Hey there, folks! Billy here, back with another tale from the trenches of applied data science. Today, we’re tackling the beast known as the mass point—a pesky cluster of values that throws off our beloved linear regression, especially after a log transformation. Spoiler alert: it’s like having a party where everyone shows up in the same outfit, and the model just can’t decide if it’s a fashion statement or a malfunction!
What the Heck Is a Mass Point?
Imagine you have a dataset where a huge number of observations are identical—say, a whole crowd buying a $1 product. When you log-transform your sales (because we love making data “normal”), those $1’s all morph into a big, fat zero (since log(1) = 0). Now your data is suddenly dominated by a mass of zeros.
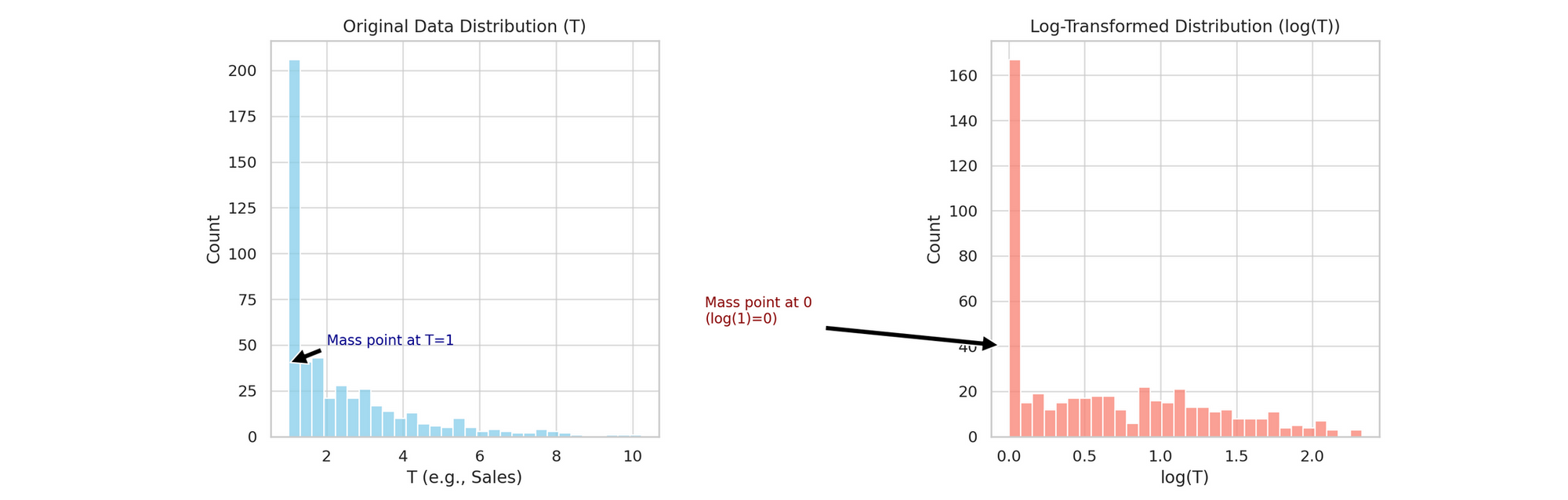
For the ones who prefer visuals: The "Mass Point" Party
- Left: A histogram of the original data showing a huge spike at T=1.
- Right: The same data after log transformation, now with a towering spike at 0.
(See Figure 1 below.)
Why Linear Models Struggle with Mass Points
Linear regression relies on several key assumptions to produce reliable results:
- Linearity: The relationship between the independent variable(s) and the dependent variable is linear.
- Independence of Errors: The residuals (errors) are independent of each other.
- Homoscedasticity: The residuals have constant variance across all levels of the independent variable(s).
- Normality: The residuals are approximately normally distributed.
When a dataset contains a mass point—a large concentration of identical values—it can violate these assumptions, particularly affecting the normality and homoscedasticity of residuals (i.e. the prediction errors of the regression model have a constant variance/spread across all levels of the independent variables, rather than changing or forming patterns).
Example: Consider a dataset where a significant number of observations have the value T=1. Applying a logarithmic transformation (commonly used to normalize data) results in log(1)=0, creating a spike at zero in the transformed data. This concentration can lead to:
- Non-Normal Residuals: The residuals may no longer follow a normal distribution due to the disproportionate influence of the mass point. For example, when a mass point exists, it can skew the residuals by introducing asymmetry or changing their spread, violating normality assumptions. Essentially, the mass point pulls the residuals toward itself, distorting their distribution instead of keeping them balanced and normally spread around zero.
- Heteroscedasticity: The variance of residuals may not remain constant, as the model struggles to account for the density at the mass point compared to other values. Ensuring homoscedasticity is important because if the variance of residuals changes—especially due to a mass point—it means the model struggles to maintain consistent accuracy across different data ranges. This can result in biased standard errors (making hypothesis tests (e.g., t-tests) unreliable), inefficient estimates (meaning the model’s predictions might not be as precise as they could be) and misleading confidence intervals (which can lead to incorrect conclusions about the significance of variables).
These issues can cause the linear model to produce biased or inefficient estimates, as it attempts to fit a linear relationship to data that doesn't adhere to its foundational assumptions.
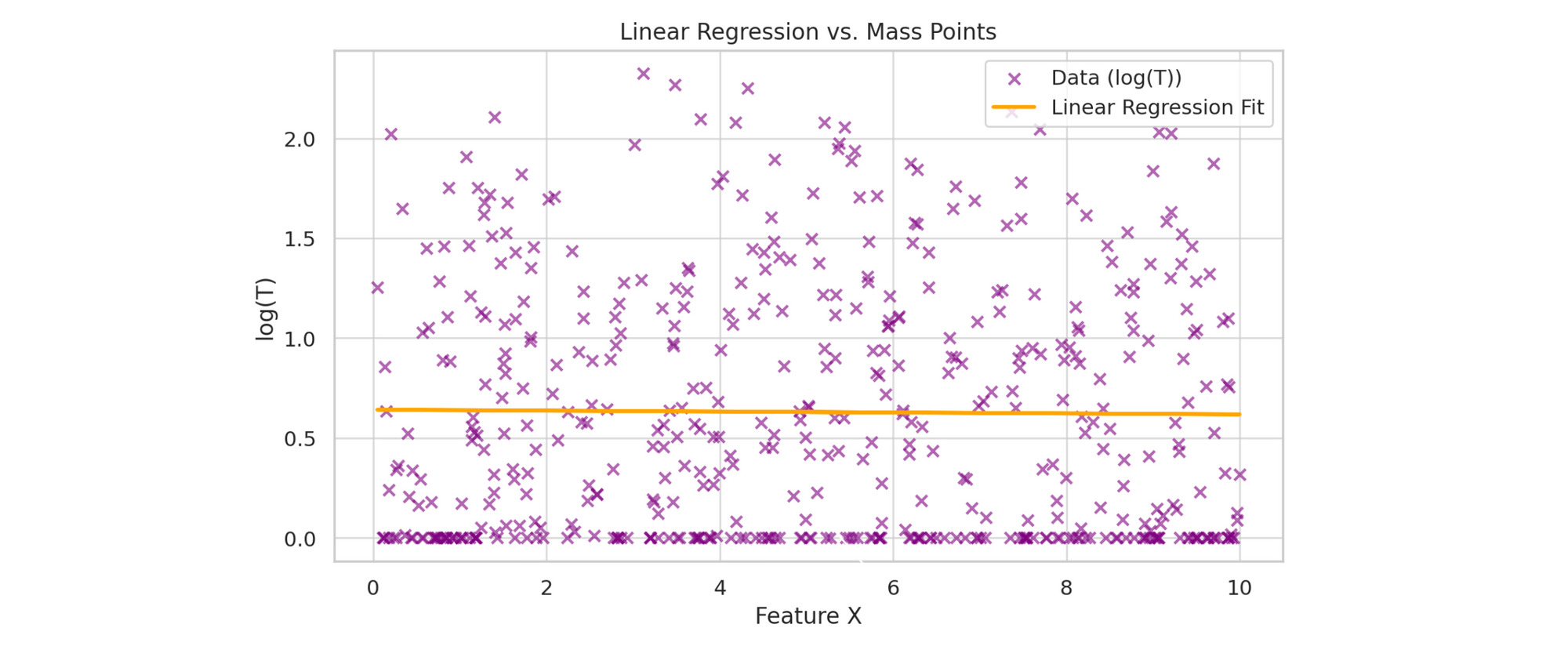
For the ones who prefer visuals: Regression vs. Mass Points
A scatter plot of our log-transformed data with a linear regression line that awkwardly skirts around the massive cluster at 0 (our fitted model gets skewed/biased towards the point mass):
Models That Know How to Party
When linear regression meets a mass point, it’s like inviting everyone to a black-tie event and having half the guests show up in the same neon T-shirt—it just doesn’t blend well. Instead, we can adopt alternative models that know how to handle these quirks and let our data have its own kind of party. Here are three possible solutions to fix the mass point problem (with their pros and cons):
| Model Type | Party Analogy (Key Idea) | Pros | Cons | When to Use It |
|---|---|---|---|---|
| Hurdle Model | Think of a two-part party: a strict bouncer (classifier) decides who belongs to the "mass point club" (e.g., those all wearing the same neon T-shirt), and only guests not in that club join the VIP lounge (regression for continuous outcomes). | - Clearly separates the party crashers from the regular guests - Makes it easy to see who’s part of the mass point group and who isn’t |
- Requires organizing two separate parts of the party - More effort to coordinate both a bouncer and a VIP lounge |
When you have a mix of mass points (e.g., a lot of (T=1) or zeros) and continuous data. |
| Mixture Model | Imagine your party is a cocktail mix: one part is a strong shot (the mass point spike), and the other is a smooth latte (the continuous values). Both flavors are mixed to create the final drink. | - Flexibly models a party with different types of guests - Captures the overall vibe by blending distinct groups |
- Can be more complex to mix properly - Finding the right blend of the shot and latte can be computationally challenging |
When your data naturally splits into distinct groups (a sharp spike mixed with a smooth distribution). |
| Zero-Inflated Model | Picture a vending machine at your party that sometimes gives out a free snack (zero) by accident. The model first checks if you’re getting a freebie (logistic component) and then, if not, charges you the usual price (continuous model). | - Specially designed for parties with too many free snacks (excess zeros) - Better fits the scenario where zeros happen more often than expected |
- Best for situations with lots of free snacks (zeros) - More complex to set up compared to a straightforward entry list |
When your data has an unusually high number of zeros (or a specific mass point) that needs special handling. |
Wrapping It All Up
When linear regression is forced to handle mass points, it’s like watching a classical dancer attempt breakdancing—awkward and off-beat. By adopting alternative approaches (hurdle, mixture, or zero-inflated models), we let the data express its natural quirks rather than forcing it into a mold it just doesn’t fit.
Next time you see a giant spike at zero in your log-transformed data, remember: sometimes you need a bouncer, a cocktail mix, or even a vending machine model to keep the party (and the predictions) lively.
Cheers, Billy!
Appendix
Impact of Heteroscedasticity on Linear Regression:
- Biased Standard Errors: When heteroscedasticity is present, the standard errors of the coefficient estimates become unreliable. This unreliability can lead to inaccurate confidence intervals and hypothesis tests, increasing the likelihood of Type I or Type II errors.
- Inefficient Estimates: Although ordinary least squares (OLS) estimators remain unbiased in the presence of heteroscedasticity, they are no longer the best linear unbiased estimators (BLUE). This inefficiency means that the estimates have higher variance than necessary, making them less precise.
Importance of Efficiency in Linear Regression
Efficiency in the context of linear regression refers to obtaining estimators with the smallest possible variance. Efficient estimators are desirable because:
- Precision: More efficient estimators provide tighter confidence intervals, enhancing the reliability of the estimates.
- Statistical Power: With increased precision, statistical tests are more likely to detect true effects when they exist, reducing the risk of Type II errors.

